5.3 Maximizing Profitap Calculus
This requires the use of maximums and minimums. We know that we find maximums and minimums via derivatives. Therefore, one can conclude that calculus will be a useful tool for maximizing or minimizing (collectively known as 'optimizing') a situation. In general, an optimization problem has a constraint that changes how we view the problem.
Combining Revenue and Costs in a Table
- In this video, we go through an example of an application problem using price, revenue, and cost functions to maximize profit.
- What calculus criterion is needed? There are two `peaks' of interest in an epidemic. 1) When are the most people sick? 2) When is the disease spreading fastest? The second peak could mean either that the rate of contracting new cases is largest or that the growth in the infectious population is largest. These are different.
- Calculus Spring 2018 Final Exam 2018-5-3 Name: Sec.: Do not remove this answer page you will turn in the entire exam. No books or notes may be used. You may use an ACT-approved calculator during the exam, but NO calculator with a Computer Algebra System (CAS), networking, or camera is permitted.
In the previous section, we analyzed profit maximization by studying graphs. In this section, we will analyze a purely competitive firm’s profit maximizing quantity based on data from a table.
The Firm’s Costs
Let’s look at the following hypothetical firm’s cost data.
| Quantity | Total Fixed Cost | Total Variable Cost | Total Cost | Marginal Cost | Average Variable Cost | Average Total Cost |
| 0 | $50 | $0 | $50 | – | – | – |
| 1 | 50 | 30 | 80 | $30 | $30 | $80 |
| 2 | 50 | 50 | 100 | 20 | 25 | 50 |
| 3 | 50 | 60 | 110 | 10 | 20 | 36.67 |
| 4 | 50 | 68 | 118 | 8 | 17 | 29.50 |
| 5 | 50 | 80 | 130 | 12 | 16 | 26 |
| 6 | 50 | 100 | 150 | 20 | 16.67 | 25 |
| 7 | 50 | 130 | 180 | 30 | 18.57 | 25.71 |
| 8 | 50 | 165 | 215 | 35 | 20.63 | 26.88 |
| 9 | 50 | 220 | 270 | 55 | 24.44 | 30 |
The Firm’s Revenue
Case A: The Market Price is above the Firm’s Average Total Cost
Let’s assume that the market price is $31. Because this firm is a purely competitive firm, marginal revenue and average revenue are also $31. Looking at the table above, we can see that at various quantities, the price exceeds the average total cost. This means that at these quantities, the firm will make a profit.
The Firm’s Profit Maximizing Quantity
In the previous section, we concluded that a firm maximizes its profits where marginal revenue equals marginal cost. Predictive text for mac. Because we have discrete data from a table rather than a continuous curve, we notice that at no quantity does the marginal revenue equal the marginal cost. In this case, we need to identify the quantity at which the marginal cost comes closest to the marginal revenue, without exceeding it. If there are values for marginal cost early on in the table, which also approach marginal revenue, do not select these. Only the marginal cost values in or approaching the increasing part of the marginal cost column are relevant. We also have to make sure that the price is above the firm’s lowest average variable cost; otherwise, it is better to shut down. The lowest variable cost in the table above is $16, so we can see that the price of $31 is, indeed, above the firm’s average variable cost. We do not have to shut down. At a quantity of 7, the marginal cost is $30, is closest to our marginal revenue of $31, and the marginal cost values are increasing. This satisfies our profit maximizing rule. Therefore, the firm maximizes profits at quantity 7. If the firm produces 7 products, it will have the most profit compared to any other quantity produced.
The Golden Rule of Profit Maximizing or Loss Minimizing Review 1ap calculus.
Let’s summarize the above information.
A firms maximizes its profits or minimizes its losses at a quantity where MC equals MR, or where a non-falling MC comes as close as possible to (without exceeding) MR. The price must be above the firm’s lowest average variable cost for the firm to produce this quantity. If the price is less than the firm’s lowest AVC, then it should shut down (produce a quantity of zero) for a while (until conditions improve). |
Case B: The Market Price is below the Firm’s Average Total Cost, but above the Firm’s Average Variable Cost
Let’s assume that market price drops to $21. This means that the firm’s average revenue and marginal revenue are $21, as well.
Looking at the table above and using the profit maximization/loss minimization rule, we see that at quantity 6, the marginal cost comes closest to the marginal revenue. The marginal cost is in the upward sloping portion of the curve. The price is above the lowest average variable cost, so we do not have to shut down. At quantity 6, the firm’s total profit equals $126 – $150 = -$24. ($126 is the total revenue: P x Q = $21 times 6; $150 is the cost at quantity 6). Thus, the firm is operating at a loss. However, producing 6 units is better than shutting down. If we shut down, our loss would be $50 (the firm’s fixed cost). A firm can incur losses during some years. However, if losses persist, it will go out of business in the long run.
Case C: The Market Price is below the Firm’s Average Total Cost and below the Firm’s Average Variable Cost
Let’s assume that the market price decreases to $15. How many products should the firm produce in order to maximize profits or minimize losses?
In this case, we notice that the price is below the firm’s lowest average variable cost. Therefore, it is best to shut down and produce a quantity of zero. The marginal cost comes closest to the marginal revenue at quantity 5. However, when you calculate total revenue minus total costs, you arrive at a loss of $55 ($75 – $130). When the firm produces at a quantity of zero, its loss is only $50 (its fixed costs).
Profit Maximizing Using Total Revenue and Total Cost Data
Instead of using the golden rule of profit maximization discussed above, you can also find a firm’s maximum profit (or minimum loss) by looking at total revenue and total cost data. Simply calculate the firm’s total revenue (price times quantity) at each quantity. Then subtract the firm’s total cost (given in the table) at each quantity. At a market price of $31, the firm’s total revenue equals $217 at a quantity of 7 ($31 times 7), and its total cost is given at $180. Therefore, the firm’s total profit at this quantity is $37. If you do the same for the other quantities, you will find that producing 7 products results in the highest profit for the firm.
Drawing Cost and Revenue Data in a Graph

If we use a market price of $31 and the cost data from the table above, and plot this data, we get

In the above example, the firm maximizes its profits when it produces 7 units, because it is where MC equals MR; ATC at this quantity is $25.71.

The vertical distance from the demand curve to the average total cost curve represents the firm’s average profit (price minus average total cost). Average profit times the number of products sold equals total profit. Thus, the profit area is the rectangle from the price ($31) down to the ATC ($25.71) and across to the vertical axis. At the profit maximizing quantity of 7 products, this is equal to the shaded area (length x width).
The Shutdown Point
The firm’s shutdown point is where its average variable cost is at its lowest value. The firm should shut down temporarily if the price drops below the shutdown price of $16. At a price below $16 the firm not only loses money on its fixed costs, but also on its variable costs. If it did operate at a price below $16, its loss would be greater than if it produced a quantity of zero (shutdown).
Video Explanation
For a video explanation of how to calculate the profit maximizing quantity and profit for a firm in pure competition, please watch:
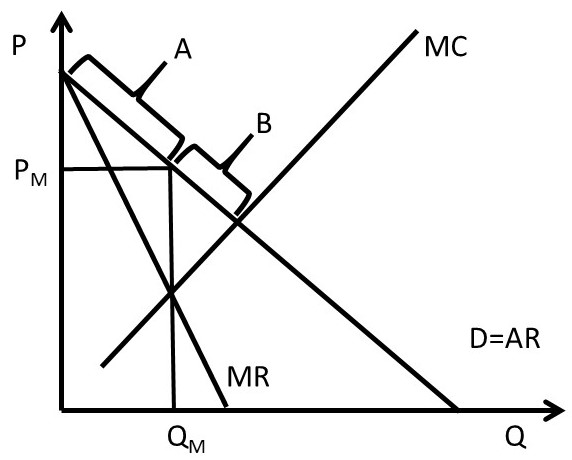
Managerial economists have studied monopolistic competition to understand how to maximize profit in that economic model. Because a monopolistically competitive firm produces a differentiated good, short-run profit maximization requires the firm to determine both the profit-maximizing quantity and the good’s price. The illustration shows short-run profit maximization for a monopolistically competitive firm.
Differentiation leads to a downward-sloping demand curve for the monopolistically competitive firm. This curve is labeled d. Because the demand curve is downward sloping, the monopolistically competitive firm must lower price in order to sell more of the good. This lower price is charged for all units of the good sold.
Marginal revenue represents the change in total revenue that occurs when one additional unit of output is produced and sold. Because the firm must charge a lower price for every unit sold in order to sell one additional unit of the good, marginal revenue is lower than the price of the last unit sold. The marginal-revenue curve, thus, lies below the demand curve, as illustrated by the curve labeled MR.
5.3 Maximizing Profitap Calculus Calculator
Marginal cost is the change in total cost that occurs when one additional unit of output is produced. Because of diminishing returns, marginal cost, MC, is upward-sloping. In addition, marginal cost passes through the minimum point of the average-total-cost curve, ATC.
The firm’s total profit increases if an additional unit of output adds more to revenue than it adds to cost. As long as the marginal revenue of an additional unit exceeds marginal cost, as is the case at qA, producing that unit increases the firm’s total profit, and the firm should continue to produce more.
On the other hand, if a unit of output adds more to cost than it adds to revenue, as with qB, or if marginal cost is greater than marginal revenue, producing that unit decreases the firm’s total profit. The firm needs to reduce production. The monopolistically competitive firm maximizes profit by producing the quantity of output associated with marginal revenue equals marginal cost.
The profit-maximizing quantity of output is represented by q0.
After determining the profit-maximizing quantity of output, the firm establishes the good’s price by going from that quantity, q0, to the demand curve and across to the vertical axis. The profit-maximizing price is P0.
5.3 Maximizing Profitap Calculus Formulas
The monopolistically competitive firm determines profit per unit by subtracting average total cost from price. In the illustration, profit per unit is represented by ð/q and equals price minus average total cost. Total profit, ð, equals profit per unit multiplied by the profit-maximizing quantity, or
