5.6 Optimization Problemsap Calculus
MAXIMUM/MINIMUM PROBLEMS
- 5.6 Optimization Problemsap Calculus Solver
- 5.6 Optimization Problemsap Calculus 2nd Edition
- 5.6 Optimization Problemsap Calculus Calculator
- 5.6 Optimization Problemsap Calculus Algebra

Here are a set of practice problems for the Calculus I notes. Click on the 'Solution' link for each problem to go to the page containing the solution.Note that some sections will have more problems than others and some will have more or less of a variety of problems. AP Calculus AB Exam and AP Calculus BC Exam, and they serve as examples of the types of questions that appear on the exam. Each question is accompanied by a table containing the main learning objective(s), essential knowledge statement(s), and Mathematical Practices for AP Calculus that the question addresses. Calculus Chapters 5 & 6. Chapter 5 Resources. Extra Optimization Problems Worksheet; Chapter 5 Extra Practice Worksheets.
The following problems are maximum/minimum optimization problems. They illustrate one of the most important applications of the first derivative. Many students find these problems intimidating because they are 'word' problems, and because there does not appear to be a pattern to these problems. However, if you are patient you can minimize your anxiety and maximize your success with these problems by following these guidelines :
GUIDELINES FOR SOLVING MAX./MIN. PROBLEMS
- 1. Read each problem slowly and carefully. Read the problem at least three times before trying to solve it. Sometimes words can be ambiguous. It is imperative to know exactly what the problem is asking. If you misread the problem or hurry through it, you have NO chance of solving it correctly.
2. If appropriate, draw a sketch or diagram of the problem to be solved. Pictures are a great help in organizing and sorting out your thoughts.
3. Define variables to be used and carefully label your picture or diagram with these variables. This step is very important because it leads directly or indirectly to the creation of mathematical equations.
4. Write down all equations which are related to your problem or diagram. Clearly denote that equation which you are asked to maximize or minimize. Experience will show you that MOST optimization problems will begin with two equations. One equation is a 'constraint' equation and the other is the 'optimization' equation. The 'constraint' equation is used to solve for one of the variables. This is then substituted into the 'optimization' equation before differentiation occurs. Some problems may have NO constraint equation. Some problems may have two or more constraint equations.
5. Before differentiating, make sure that the optimization equation is a function of only one variable. Then differentiate using the well-known rules of differentiation.
6. Verify that your result is a maximum or minimum value using the first or second derivative test for extrema.
The following problems range in difficulty from average to challenging.
- PROBLEM 1 : Find two nonnegative numbers whose sum is 9 and so that the product of one number and the square of the other number is a maximum.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Build a rectangular pen with three parallel partitions using 500 feet of fencing. What dimensions will maximize the total area of the pen ?
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : An open rectangular box with square base is to be made from 48 ft.2 of material. What dimensions will result in a box with the largest possible volume ?
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : A container in the shape of a right circular cylinder with no top has surface area 3ft.2 What height h and base radius r will maximize the volume of the cylinder ?
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : A sheet of cardboard 3 ft. by 4 ft. will be made into a box by cutting equal-sized squares from each corner and folding up the four edges. What will be the dimensions of the box with largest volume ?
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Consider all triangles formed by lines passing through the point (8/9, 3) and both the x- and y-axes. Find the dimensions of the triangle with the shortest hypotenuse.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Find the point (x, y) on the graph of nearest the point (4, 0).
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : A cylindrical can is to hold 20m.3 The material for the top and bottom costs $10/m.2 and material for the side costs $8/m.2 Find the radius r and height h of the most economical can.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : You are standing at the edge of a slow-moving river which is one mile wide and wish to return to your campground on the opposite side of the river. You can swim at 2 mph and walk at 3 mph. You must first swim across the river to any point on the opposite bank. From there walk to the campground, which is one mile from the point directly across the river from where you start your swim. What route will take the least amount of time ?
Click HERE to see a detailed solution to problem 9.
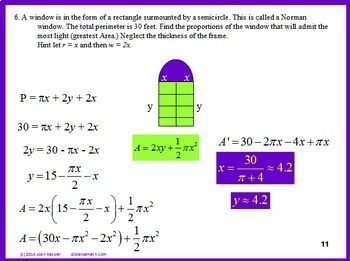
- PROBLEM 10 : Construct a window in the shape of a semi-circle over a rectangle. If the distance around the outside of the window is 12 feet, what dimensions will result in the rectangle having largest possible area ?
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : There are 50 apple trees in an orchard. Each tree produces 800 apples. For each additional tree planted in the orchard, the output per tree drops by 10 apples. How many trees should be added to the existing orchard in order to maximize the total output of trees ?
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Find the dimensions of the rectangle of largest area which can be inscribed in the closed region bounded by the x-axis, y-axis, and graph of y=8-x3 . (See diagram.)
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Consider a rectangle of perimeter 12 inches. Form a cylinder by revolving this rectangle about one of its edges. What dimensions of the rectangle will result in a cylinder of maximum volume ?
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : A movie screen on a wall is 20 feet high and 10 feet above the floor. At what distance x from the front of the room should you position yourself so that the viewing angle of the movie screen is as large as possible ? (See diagram.)
Click HERE to see a detailed solution to problem 14.
- PROBLEM 15 : Find the dimensions (radius r and height h) of the cone of maximum volume which can be inscribed in a sphere of radius 2.
Click HERE to see a detailed solution to problem 15.
- PROBLEM 16 : What angle between two edges of length 3 will result in an isosceles triangle with the largest area ? (See diagram.)
Click HERE to see a detailed solution to problem 16.
- PROBLEM 17 : Of all lines tangent to the graph of , find the tangent lines of mimimum slope and maximum slope.
Click HERE to see a detailed solution to problem 17.
- PROBLEM 18 : Find the length of the shortest ladder that will reach over an 8-ft. high fence to a large wall which is 3 ft. behind the fence. (See diagram.)
Click HERE to see a detailed solution to problem 18.
- PROBLEM 19 : Find the point P = (x, 0) on the x-axis which minimizes the sum of the squares of the distances from P to (0, 0) and from P to (3, 2).
Click HERE to see a detailed solution to problem 19.
- PROBLEM 20 : Car B is 30 miles directly east of Car A and begins moving west at 90 mph. At the same moment car A begins moving north at 60 mph. What will be the minimum distance between the cars and at what time t does the minimum distance occur ?
Click HERE to see a detailed solution to problem 20.
- PROBLEM 21 : A rectangular piece of paper is 12 inches high and six inches wide. The lower right-hand corner is folded over so as to reach the leftmost edge of the paper (See diagram.).
Find the minimum length of the resulting crease.
Netflix. Click HERE to see a detailed solution to problem 21.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :
Duane Kouba5.6 Optimization Problemsap Calculus Solver
1998-06-16Show Mobile NoticeShow All NotesHide All Notes
Here are a set of practice problems for the Calculus I notes. Click on the 'Solution' link for each problem to go to the page containing the solution.
Note that some sections will have more problems than others and some will have more or less of a variety of problems. Most sections should have a range of difficulty levels in the problems although this will vary from section to section.
Here is a listing of sections for which practice problems have been written as well as a brief description of the material covered in the notes for that particular section.
Review - In this chapter we give a brief review of selected topics from Algebra and Trig that are vital to surviving a Calculus course. Included are Functions, Trig Functions, Solving Trig Equations and Equations, Exponential/Logarithm Functions and Solving Exponential/Logarithm Equations.Inverse Functions – In this section we will define an inverse function and the notation used for inverse functions. We will also discuss the process for finding an inverse function.
Trig Functions – In this section we will give a quick review of trig functions. We will cover the basic notation, relationship between the trig functions, the right triangle definition of the trig functions. We will also cover evaluation of trig functions as well as the unit circle (one of the most important ideas from a trig class!) and how it can be used to evaluate trig functions.
Solving Trig Equations – In this section we will discuss how to solve trig equations. The answers to the equations in this section will all be one of the “standard” angles that most students have memorized after a trig class. However, the process used here can be used for any answer regardless of it being one of the standard angles or not.
Solving Trig Equations with Calculators, Part I – In this section we will discuss solving trig equations when the answer will (generally) require the use of a calculator (i.e. they aren’t one of the standard angles). Note however, the process used here is identical to that for when the answer is one of the standard angles. The only difference is that the answers in here can be a little messy due to the need of a calculator. Included is a brief discussion of inverse trig functions.
Solving Trig Equations with Calculators, Part II – In this section we will continue our discussion of solving trig equations when a calculator is needed to get the answer. The equations in this section tend to be a little trickier than the 'normal' trig equation and are not always covered in a trig class.
Exponential Functions –In this section we will discuss exponential functions. We will cover the basic definition of an exponential function, the natural exponential function, i.e. ({bf e}^{x}), as well as the properties and graphs of exponential functions
Logarithm Functions – In this section we will discuss logarithm functions, evaluation of logarithms and their properties. We will discuss many of the basic manipulations of logarithms that commonly occur in Calculus (and higher) classes. Included is a discussion of the natural ((ln(x))) and common logarithm ((log(x))) as well as the change of base formula.
Exponential and Logarithm Equations – In this section we will discuss various methods for solving equations that involve exponential functions or logarithm functions.
Common Graphs – In this section we will do a very quick review of many of the most common functions and their graphs that typically show up in a Calculus class.
Limits - In this chapter we introduce the concept of limits. We will discuss the interpretation/meaning of a limit, how to evaluate limits, the definition and evaluation of one-sided limits, evaluation of infinite limits, evaluation of limits at infinity, continuity and the Intermediate Value Theorem. We will also give a brief introduction to a precise definition of the limit and how to use it to evaluate limits
The Limit – In this section we will introduce the notation of the limit. We will also take a conceptual look at limits and try to get a grasp on just what they are and what they can tell us. We will be estimating the value of limits in this section to help us understand what they tell us. We will actually start computing limits in a couple of sections.
One-Sided Limits – In this section we will introduce the concept of one-sided limits. We will discuss the differences between one-sided limits and limits as well as how they are related to each other.
Limit Properties – In this section we will discuss the properties of limits that we’ll need to use in computing limits (as opposed to estimating them as we've done to this point). We will also compute a couple of basic limits in this section.
Computing Limits – In this section we will looks at several types of limits that require some work before we can use the limit properties to compute them. We will also look at computing limits of piecewise functions and use of the Squeeze Theorem to compute some limits.
Infinite Limits – In this section we will look at limits that have a value of infinity or negative infinity. We’ll also take a brief look at vertical asymptotes.
Limits At Infinity, Part I – In this section we will start looking at limits at infinity, i.e. limits in which the variable gets very large in either the positive or negative sense. We will concentrate on polynomials and rational expressions in this section. We’ll also take a brief look at horizontal asymptotes.
Limits At Infinity, Part II – In this section we will continue covering limits at infinity. We’ll be looking at exponentials, logarithms and inverse tangents in this section.
Continuity – In this section we will introduce the concept of continuity and how it relates to limits. We will also see the Intermediate Value Theorem in this section and how it can be used to determine if functions have solutions in a given interval.
The Definition of the Limit – In this section we will give a precise definition of several of the limits covered in this section. We will work several basic examples illustrating how to use this precise definition to compute a limit. We’ll also give a precise definition of continuity.
 Derivatives - In this chapter we introduce Derivatives. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation.
Derivatives - In this chapter we introduce Derivatives. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. Interpretation of the Derivative – In this section we give several of the more important interpretations of the derivative. We discuss the rate of change of a function, the velocity of a moving object and the slope of the tangent line to a graph of a function.
Differentiation Formulas – In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. Examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.
Product and Quotient Rule – In this section we will give two of the more important formulas for differentiating functions. We will discuss the Product Rule and the Quotient Rule allowing us to differentiate functions that, up to this point, we were unable to differentiate.
Derivatives of Trig Functions – In this section we will discuss differentiating trig functions. Derivatives of all six trig functions are given and we show the derivation of the derivative of (sin(x)) and (tan(x)).
Derivatives of Exponential and Logarithm Functions – In this section we derive the formulas for the derivatives of the exponential and logarithm functions.
Derivatives of Inverse Trig Functions – In this section we give the derivatives of all six inverse trig functions. We show the derivation of the formulas for inverse sine, inverse cosine and inverse tangent.
Derivatives of Hyperbolic Functions – In this section we define the hyperbolic functions, give the relationships between them and some of the basic facts involving hyperbolic functions. We also give the derivatives of each of the six hyperbolic functions and show the derivation of the formula for hyperbolic sine.
Chain Rule – In this section we discuss one of the more useful and important differentiation formulas, The Chain Rule. With the chain rule in hand we will be able to differentiate a much wider variety of functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you take will involve the chain rule!
Implicit Differentiation – In this section we will discuss implicit differentiation. Not every function can be explicitly written in terms of the independent variable, e.g. y = f(x) and yet we will still need to know what f'(x) is. Implicit differentiation will allow us to find the derivative in these cases. Knowing implicit differentiation will allow us to do one of the more important applications of derivatives, Related Rates (the next section).
Related Rates – In this section we will discuss the only application of derivatives in this section, Related Rates. In related rates problems we are give the rate of change of one quantity in a problem and asked to determine the rate of one (or more) quantities in the problem. This is often one of the more difficult sections for students. We work quite a few problems in this section so hopefully by the end of this section you will get a decent understanding on how these problems work.
Higher Order Derivatives – In this section we define the concept of higher order derivatives and give a quick application of the second order derivative and show how implicit differentiation works for higher order derivatives.
Logarithmic Differentiation – In this section we will discuss logarithmic differentiation. Logarithmic differentiation gives an alternative method for differentiating products and quotients (sometimes easier than using product and quotient rule). More importantly, however, is the fact that logarithm differentiation allows us to differentiate functions that are in the form of one function raised to another function, i.e. there are variables in both the base and exponent of the function.
5.6 Optimization Problemsap Calculus 2nd Edition
Applications of Derivatives - In this chapter we will cover many of the major applications of derivatives. Applications included are determining absolute and relative minimum and maximum function values (both with and without constraints), sketching the graph of a function without using a computational aid, determining the Linear Approximation of a function, L’Hospital’s Rule (allowing us to compute some limits we could not prior to this), Newton's Method (allowing us to approximate solutions to equations) as well as a few basic Business applications.Critical Points – In this section we give the definition of critical points. Critical points will show up in most of the sections in this chapter, so it will be important to understand them and how to find them. We will work a number of examples illustrating how to find them for a wide variety of functions.
Minimum and Maximum Values – In this section we define absolute (or global) minimum and maximum values of a function and relative (or local) minimum and maximum values of a function. It is important to understand the difference between the two types of minimum/maximum (collectively called extrema) values for many of the applications in this chapter and so we use a variety of examples to help with this. We also give the Extreme Value Theorem and Fermat's Theorem, both of which are very important in the many of the applications we'll see in this chapter.
Finding Absolute Extrema – In this section we discuss how to find the absolute (or global) minimum and maximum values of a function. In other words, we will be finding the largest and smallest values that a function will have.
The Shape of a Graph, Part I – In this section we will discuss what the first derivative of a function can tell us about the graph of a function. The first derivative will allow us to identify the relative (or local) minimum and maximum values of a function and where a function will be increasing and decreasing. We will also give the First Derivative test which will allow us to classify critical points as relative minimums, relative maximums or neither a minimum or a maximum.
The Shape of a Graph, Part II – In this section we will discuss what the second derivative of a function can tell us about the graph of a function. The second derivative will allow us to determine where the graph of a function is concave up and concave down. The second derivative will also allow us to identify any inflection points (i.e. where concavity changes) that a function may have. We will also give the Second Derivative Test that will give an alternative method for identifying some critical points (but not all) as relative minimums or relative maximums.
The Mean Value Theorem – In this section we will give Rolle's Theorem and the Mean Value Theorem. With the Mean Value Theorem we will prove a couple of very nice facts, one of which will be very useful in the next chapter.
Optimization Problems – In this section we will be determining the absolute minimum and/or maximum of a function that depends on two variables given some constraint, or relationship, that the two variables must always satisfy. We will discuss several methods for determining the absolute minimum or maximum of the function. Examples in this section tend to center around geometric objects such as squares, boxes, cylinders, etc.
More Optimization Problems – In this section we will continue working optimization problems. The examples in this section tend to be a little more involved and will often involve situations that will be more easily described with a sketch as opposed to the 'simple' geometric objects we looked at in the previous section.
L’Hospital’s Rule and Indeterminate Forms – In this section we will revisit indeterminate forms and limits and take a look at L’Hospital’s Rule. L’Hospital’s Rule will allow us to evaluate some limits we were not able to previously.
Linear Approximations – In this section we discuss using the derivative to compute a linear approximation to a function. We can use the lienar approximation to a function to approximate values of the function at certain points. While it might not seem like a useful thing to do with when we have the function there really are reasons that one might want to do this. We give two ways this can be useful in the examples.
Differentials – In this section we will compute the differential for a function. We will give an application of differentials in this section. However, one of the more important uses of differentials will come in the next chapter and unfortunately we will not be able to discuss it until then.
Newton’s Method – In this section we will discuss Newton's Method. Newton's Method is an application of derivatives will allow us to approximate solutions to an equation. There are many equations that cannot be solved directly and with this method we can get approximations to the solutions to many of those equations.
Business Applications – In this section we will give a cursory discussion of some basic applications of derivatives to the business field. We will revisit finding the maximum and/or minimum function value and we will define the marginal cost function, the average cost, the revenue function, the marginal revenue function and the marginal profit function. Note that this section is only intended to introduce these concepts and not teach you everything about them.
Integrals - In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of each type of integral as well as how to compute them including the Substitution Rule. We will give the Fundamental Theorem of Calculus showing the relationship between derivatives and integrals. We will also discuss the Area Problem, an important interpretation of the definite integral.
Computing Indefinite Integrals – In this section we will compute some indefinite integrals. The integrals in this section will tend to be those that do not require a lot of manipulation of the function we are integrating in order to actually compute the integral. As we will see starting in the next section many integrals do require some manipulation of the function before we can actually do the integral. We will also take a quick look at an application of indefinite integrals.
Substitution Rule for Indefinite Integrals – In this section we will start using one of the more common and useful integration techniques – The Substitution Rule. With the substitution rule we will be able integrate a wider variety of functions. The integrals in this section will all require some manipulation of the function prior to integrating unlike most of the integrals from the previous section where all we really needed were the basic integration formulas.
More Substitution Rule – In this section we will continue to look at the substitution rule. The problems in this section will tend to be a little more involved than those in the previous section.
Area Problem – In this section we start off with the motivation for definite integrals and give one of the interpretations of definite integrals. We will be approximating the amount of area that lies between a function and the (x)-axis. As we will see in the next section this problem will lead us to the definition of the definite integral and will be one of the main interpretations of the definite integral that we'll be looking at in this material.
Definition of the Definite Integral – In this section we will formally define the definite integral, give many of its properties and discuss a couple of interpretations of the definite integral. We will also look at the first part of the Fundamental Theorem of Calculus which shows the very close relationship between derivatives and integrals
Computing Definite Integrals – In this section we will take a look at the second part of the Fundamental Theorem of Calculus. This will show us how we compute definite integrals without using (the often very unpleasant) definition. The examples in this section can all be done with a basic knowledge of indefinite integrals and will not require the use of the substitution rule. Included in the examples in this section are computing definite integrals of piecewise and absolute value functions.
Substitution Rule for Definite Integrals – In this section we will revisit the substitution rule as it applies to definite integrals. The only real requirements to being able to do the examples in this section are being able to do the substitution rule for indefinite integrals and understanding how to compute definite integrals in general.
5.6 Optimization Problemsap Calculus Calculator
Applications of Integrals - In this chapter we will take a look at some applications of integrals. We will look at Average Function Value, Area Between Curves, Volume (both solids of revolution and other solids) and Work.
Area Between Curves – In this section we’ll take a look at one of the main applications of definite integrals in this chapter. We will determine the area of the region bounded by two curves.
Volumes of Solids of Revolution / Method of Rings – In this section, the first of two sections devoted to finding the volume of a solid of revolution, we will look at the method of rings/disks to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
Volumes of Solids of Revolution / Method of Cylinders – In this section, the second of two sections devoted to finding the volume of a solid of revolution, we will look at the method of cylinders/shells to find the volume of the object we get by rotating a region bounded by two curves (one of which may be the (x) or (y)-axis) around a vertical or horizontal axis of rotation.
More Volume Problems – In the previous two sections we looked at solids that could be found by treating them as a solid of revolution. Not all solids can be thought of as solids of revolution and, in fact, not all solids of revolution can be easily dealt with using the methods from the previous two sections. So, in this section we’ll take a look at finding the volume of some solids that are either not solids of revolutions or are not easy to do as a solid of revolution.
Work – In this section we will look at is determining the amount of work required to move an object subject to a force over a given distance.
5.6 Optimization Problemsap Calculus Algebra
